C - 最小全域木?なにそれおいしいの?
Earlgray
2
s
1024
MB
300
点
問題文
$N$ 個の街を相互に行き来可能とするように街道を作りたいです。
具体的には、各街からいくつかの街と街道を通って、すべての街へ行けるようにしたいです。
今、街を $1,2,...,N$ として、2 つの街 $(i, j)$ 同士をつなぐ街道に対するコスト $C_{i, j}$ が以下のように推定されています。
- $C_{i, j} = i+j\ (i \neq j, 1 \leq i,j \leq N)$
この時、$N-1$ 個の街道を建設して、$N$ 個の街が相互に行き来可能となるようにするために必要なコストの最小値を求めなさい。
余談
$N$ 個以上の街道を建設すると最小のコストにはならないことは示せます。このような問題は一般に最小全域木と呼ばれ、AtCoderでは500点以上の問題に出題されることが多いです。 ただし、この問題を解くには最小全域木のアルゴリズムは必要なく、想定解の1つは $О(1)$ です。 もちろん、最小全域木のアルゴリズムを用いても解くことが出来ます。
ヒント
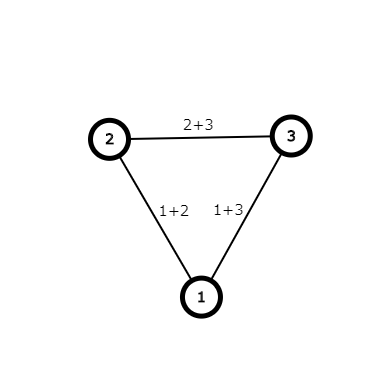
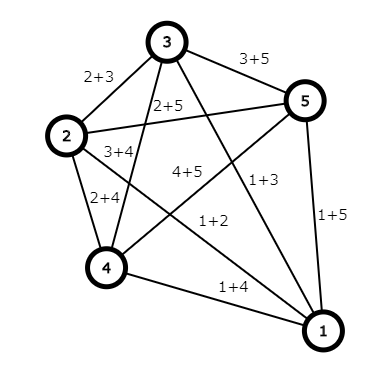
- $N=3$,$N=5$ の時のサンプルの図を見て、どの街道を選べば最小のコストになるかを考えてみる。
- $N$ と $N+1$ の答えに法則性があるかを考えてみる。
- 最小コストになる街道の繋げ方には決まりがある?
といったことを考えてみましょう。以下のようにしても良いですが、UnionFind等の知識が必要になり、難易度は高いです。
- 最小全域木のアルゴリズムを調べて貼る。(上級者向け)
制約
- $3 \leq N \leq 10^3$
- $N$ は整数
入力
入力は以下の形式で標準入力から与えられる。
$N$
出力
コストが最小となるように街道を作った際に必要なコストを出力せよ。
入力例 1
3
出力例 1
7
街1,2をつなぐ街道と街3,1をつなぐ街道を作ることで、全ての街は街道を通って相互に行き来可能となります。
また、これよりコストの総和が少なくなる街道の選び方はありません。
入力例 2
5
出力例 2
18
入力例 3
99
出力例 3
5047