D - Can you see those skyscrapers?
問題文
Writerの想定解に誤りがございました.大変申し訳ございません.
現在修正作業が完了し,正しい正誤判定がなされます.
sqrt10 くんは南北方向と高さ方向の 2 次元平面内にいます.南北方向に $N$ 個のビル $1, \dots, N$ がこの順に北から一直線に,重なることなく間を空けて並んでいます.ビル $i\ (i=1, \dots, N)$ の高さは $h_i$, 北端の座標は $a_i$, 南端の座標は $b_i$ です.
sqrt10 くんはビル $K\ (1\leq K\leq N)$ の屋上にいます.sqrt10 くんはビルが好きなので,屋上からビルが何個見えるか数えています.しかし,手前にあるビルにより奥のビルが隠されてしまっている(完全に重なって見えている場合も含みます)場合,奥のビルは見ることができません.sqrt10 くんはこのビルの屋上の上(つまり,区間 $[a_K, b_K]$)を自由に移動できるとして,見ることのできるビルはビル $K$ の他に何個ありますか? なお,ビル $K$ の屋上の上のある 1 ヶ所を固定して,そこから見ることのできるビルの数を数えるのではなく,各ビルで同じとは限らない,少なくとも 1 ヶ所から見ることのできるビルの数を数えてください.
ただし,sqrt10 くんの目線の高さはビル $K$ の屋上の高さから 1 高いところにある ものとします.また,sqrt10 くんの南北方向の身体の幅は 0 であるとして構いません.sqrt10 くんはとても目が良いので,どんなに遠くてもビルをはっきりと見ることができます.
制約
- 入力はすべて整数
- $2 \leq N\leq 10^5$
- $1 \leq K \leq N$
- $1 \leq h_i, a_i, b_i \leq 10^6\ (1\leq i\leq N)$
- $a_i<b_i\ (1\leq i\leq N)$
- $b_i<a_{i+1}\ (1\leq i\leq N-1)$
入力
$N\ K$
$h_1\ a_1\ b_1$
$\vdots$
$h_N\ a_N\ b_N$
出力
見ることができるビルの個数が何個か,整数で出力してください.
5 3
14 1 3
12 4 5
8 6 10
7 12 14
5 15 16
3
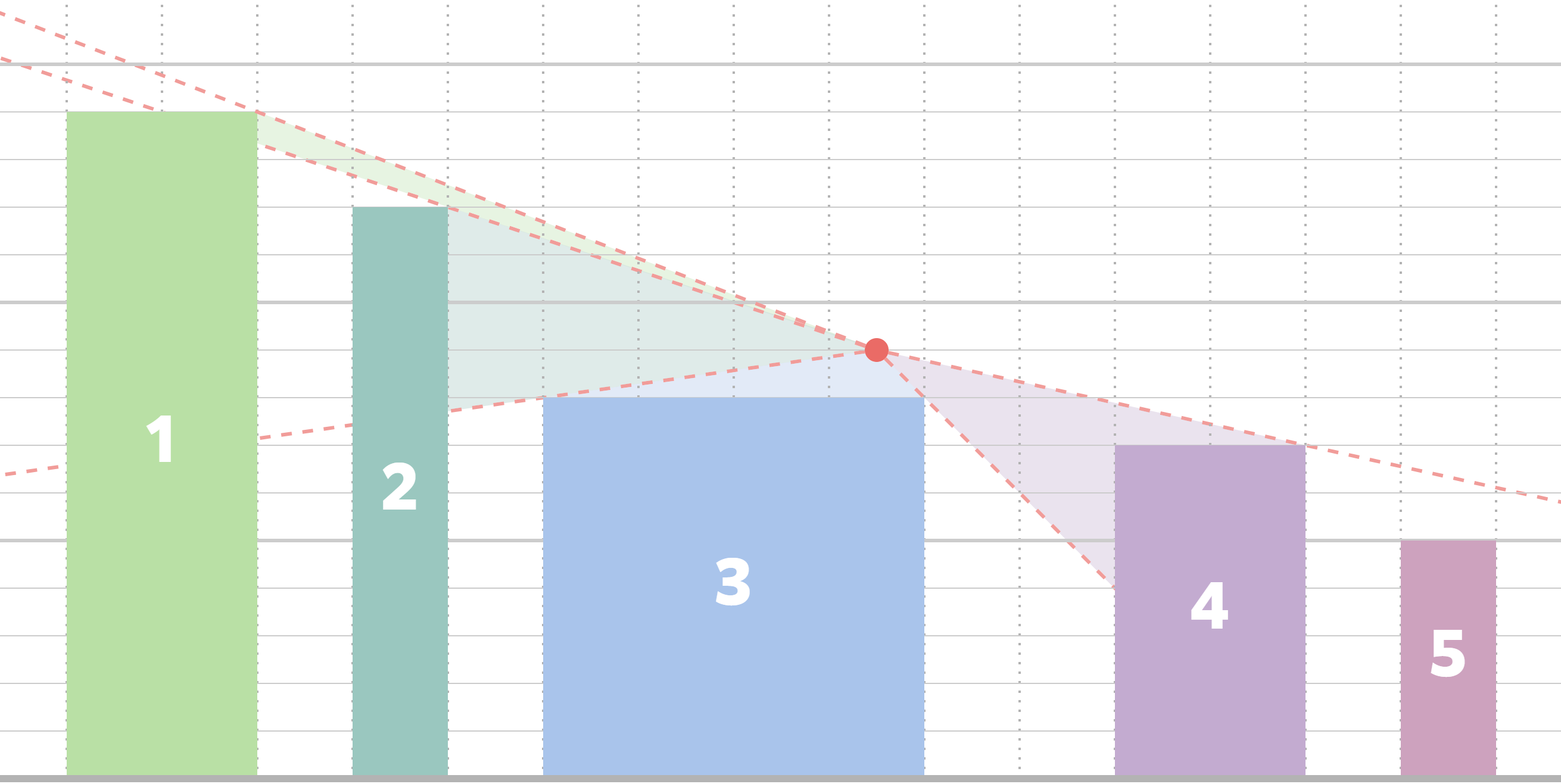
ビル 2,ビル 4 が見られることはすぐわかります.ビル 1 については,座標 7 にいてもビル 2 に隠れて見えませんが,例えば座標 9 に移動すれば見ることができます(目線の高さは $8+1=9$ にあることに注意してください).ビル 5 については,見下ろす形になりますが,どこにいてもビル 4 に隠されて見ることができません.よってビル 3 以外に見ることができるのはビル 1, 2, 4 の 3 つです.
下の図では,ビル 3 の上の座標 9.5 からビル 1, 2, 4 が見えてる様子を表しています.
5 3
14 1 3
12 4 5
8 6 10
12 11 12
14 13 15
4
ビル 1 とビル 4 を同時に見ることができる場所は存在しませんが,別々に見ることができる場所はそれぞれ存在するので,いずれも「見ることができる」ことになります.
3 1
5 1 2
6 3 4
6 5 6
1
ビル 1 の上のどこにいても,ビル 3 はビル 2 にぴったり重なって見えます.このような場合ビル 3 は見えることになりません.