J - How many K-gon?
Ceylon
2
s
1024
MB
900
点
問題文
ある円があり、その円周を $N$ 等分するように点が $N$ 個あります。
これらの点の中から相異なる点を $K$ 個選ぶと、この $K$ 点を頂点とする凸多角形は一意に定まります。このようにして作ることのできる凸多角形は何種類あるでしょうか? $10^9+7$ で割ったあまりを求めてください。
ただし、$2$ つの凸多角形は、$2$ つが合同であるときかつそのときに限り、同じ種類であるとみなします。
制約
- $3 \leq N \leq 10^{9}$
- $3 \leq K \leq \min(10^{7}, N)$
- 入力はすべて整数
部分点
この問題はいくつかの小課題に分けられ、その小課題のすべてのテストケースに正解した場合に「この小課題に正解した」とみなされます。
提出したソースコードの得点は、正解した小課題の点数の合計となります。
- (100点) $N \leq 10$
- (150点) $K = 3$
- (250点) $N \leq 10^5$
- (400点) 追加の制約はない
入力
入力は以下の形式で標準入力から与えられます。
$N$ $K$
出力
答えを $1$ 行で出力せよ。
入力例 1
12 3
出力例 1
12
考えうる図形は、以下の $12$ 個とそれらと合同な図形です。
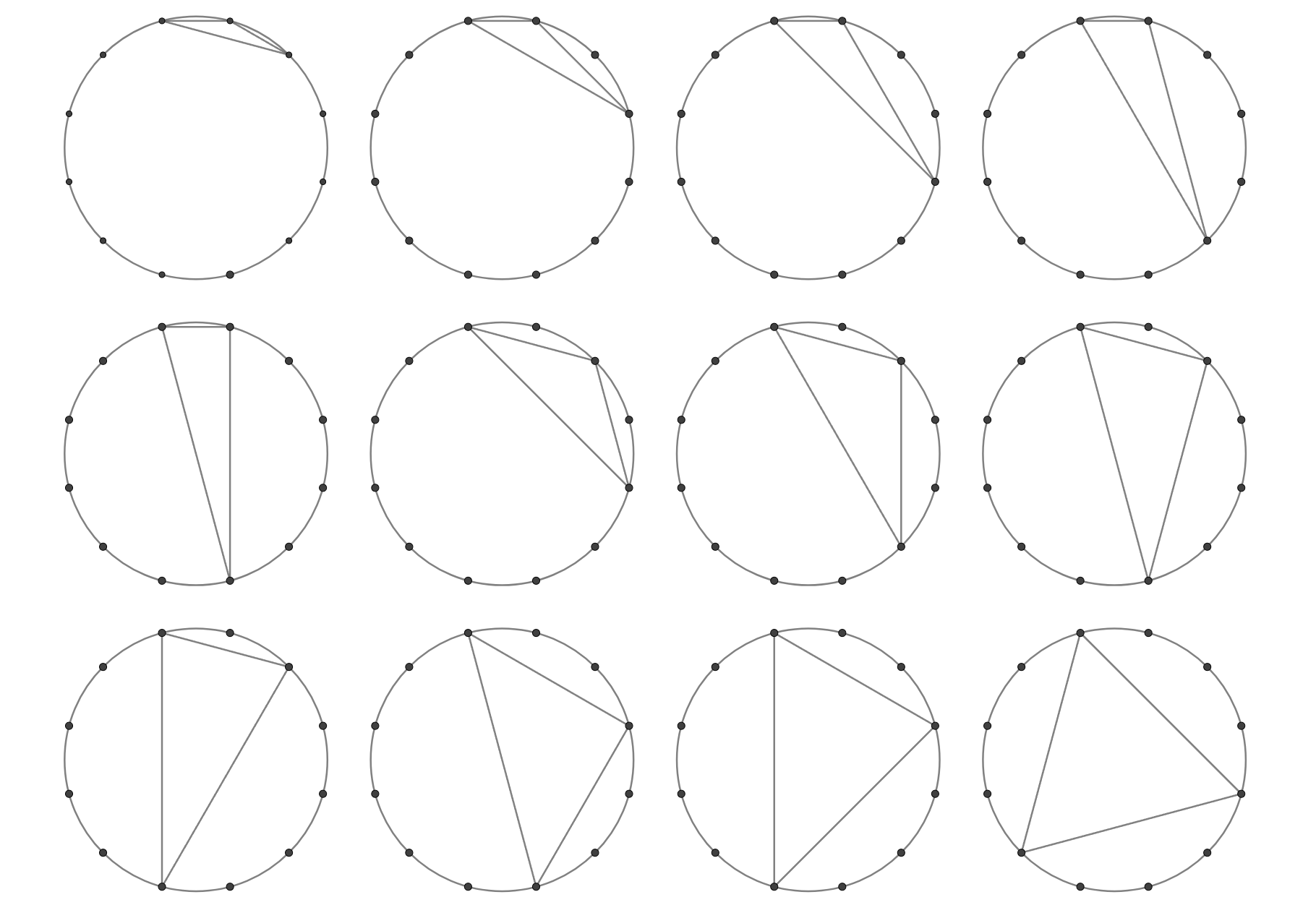
入力例 2
6 3
出力例 2
3
入力例 3
50 30
出力例 3
293786219
入力例 4
998244353 3141592
出力例 4
122221167
$10^9 + 7$ で割ったあまりを出力してください。